Origin of temporaly stable particles
Rotation: The world we perceive is based on small entities that orbit themselves and thus form stable structures over time like photons (Sonon). Multiple rotating Sonons create stable structures in space and time forming the basis for matter like electrons or protons.
Universe: The whole universe consists of rotating objects (Rotons), which create forces between themselves - in a layered structure of rotations of different magnitudes like: photon, electron, atom, solar systems, galaxies, universe.
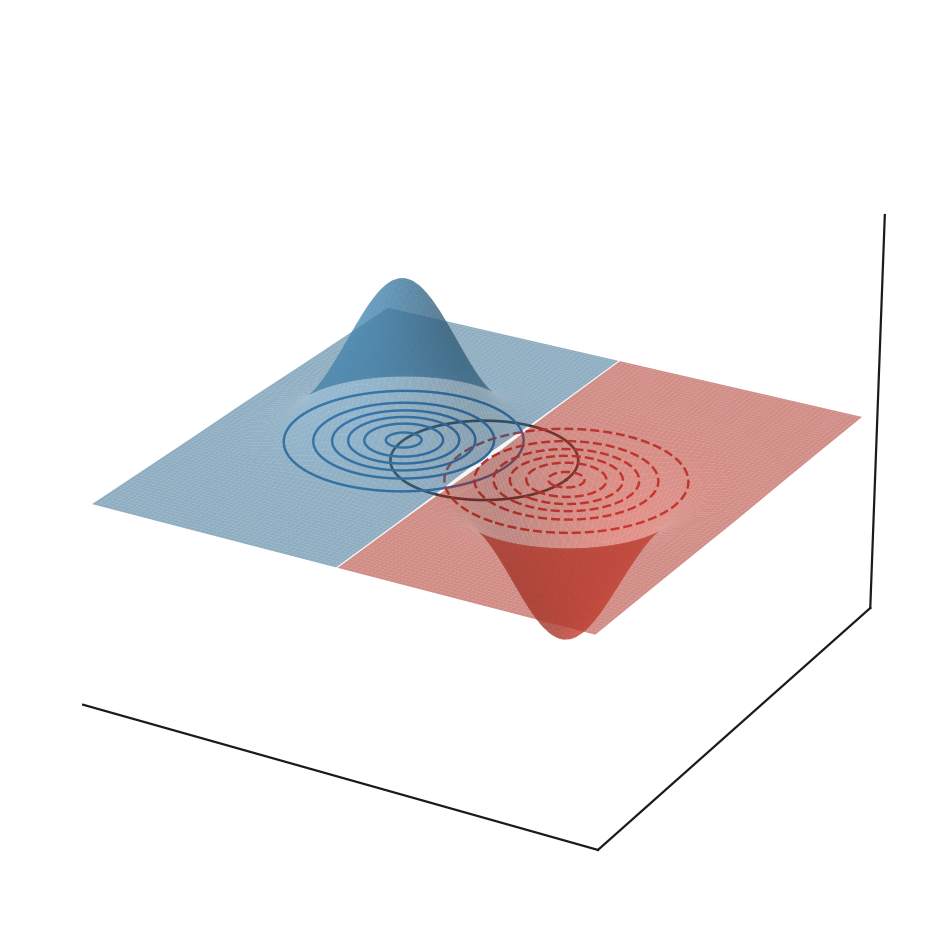
LEDO-Field = Lambda Energy Density Oscillation (LEDO)
Abstract
The Lambda Energy Density Oscillation (LEDO) Field is a wavelength-resolved field of local energy density, carrying not just scalar amplitude but the spectral composition and gradients of overlapping oscillations.
Definition
Lambda Energy Density Oscillation (LEDO) designates a field concept in which local energy density is not confined to a single harmonic mode but unfolds as a superposed spectrum of wavelength-resolved oscillations. Individual modulations flow, interweave, and resonate, embedding not only a scalar value but also information about the frequency composition and gradient at each point in space.
Here, Lambda explicitly denotes wavelength awareness: the field carries a spectral decomposition akin to a local Fourier content, such that different frequency components remain distinguishable even while overlapping. This enables instant, scale-dependent and direction-dependent interactions — local energy density contributes to a total value and gradient, while the spectral separation allows wavelength-specific coupling and resonance to occur across arbitrary distances.
Locally this simply contributes to a total energy density value and gradient. The frequency separation and its awareness allows for wavelength individual interactions over arbitrary distances. Such rotating modulations lead to resonances in other locations of the LEDO-Field inferring de-localized oscillations.
Physical decomposition (for the physical correctness)
To indicate different aspects of the LEDO field we introduce the following projections of its state:
- A resonance potential field (ADR)
- A gyroscopic inertia response field (IGT)
- An energy density transition (EDT), the effective rotonal-inertia flow, the product of the DRI x IGT onto the resonance source area
- Result: An energy density oscillation field (LEDO) showing wave-like transitions of self-resonant entities in physical spacetime
Discussion - difference to a scalar or vector field
Through rotational modulations, the LEDO field can sustain non-local resonances: oscillatory patterns from one place induce correlated responses elsewhere, rendering the field an inherently wavelength-sensitive, frequency-structured and directionally resolved representation of energy oscillations.
Discussion - instantaneous aspect
The DRI part of the LEDO field provides instantaneous impact with NO time delay. Why is this needed? A resonance across spacetime has to be consistent along the whole direction. In addition the initially modeled wave-like structure of the LEDO-Field is intuitive but not accurate to result in effective attraction. What the LEDO field does is impose a rotational resonance (think of it as a rotatory force) onto a target Roton. A resulting observed attraction between energy manifestations though, is only the result of the precession preventing energy pressure to move the gyroscope in radial direction. Instead the Roton will accelerate into axial direction.
Scalar Field vs. LEDO Field
Differences:
- Scalar field: total value $\rho(x,t)$ only. Overlapping gradient can be calculated via surrounding.
- Local FFT: $\tilde{\rho}(x,\omega)$ reveals frequency content, but loses spatially and directionally resolved detail.
- LEDO field: retains $\rho_\lambda(x,t)$ (directional) and $\nabla \rho_\lambda(x,t)$ (frequency) of the resoance making the field spectral aware and capable of wavelength-specific interactions in different directions.
In short:
LEDO = frequency spectrum aware, directional resonant oscillation of local energy density
| Aspect |
Scalar Field ($\rho(x,t)$) |
LEDO Field ($\Lambda$-Energy Density Oscillation) |
| Stored quantity |
Single local energy density value |
Wavelength-resolved decomposition ${\rho_\lambda(x,t), \nabla\rho_\lambda(x,t)}_\lambda$ |
| Frequency awareness |
Hidden in total oscillation; requires FFT to extract |
Explicit per-wavelength contributions available at each point |
| Spatial information |
Only total gradient $\nabla\rho$ |
Gradient and phase per wavelength, revealing scale-specific flows |
| Overlapping components |
Can cancel or mask each other in the sum |
Remain distinguishable; overlapping λ’s can be tracked individually |
| Resonances & coupling |
Hard to identify beyond local oscillations |
Enables λ-specific, nonlocal resonances across space |
| Analogy |
Temperature of a gas (average only) |
Full velocity distribution (spectral structure) |
Please find below a few visualizations for the discussed topic.
REMARK: IMPROVE VISUALIZATIONS, THEY ARE NOT MATCHING THE TEXT
Peak Visualization
 3D visualization of a single scalar field with overlapping waves of different frequencies
3D visualization of a single scalar field with overlapping waves of different frequencies
Rotons of different magnitude
 This is a 2D cut from an overlapped modulation of superposed LEDO-Field. Static Rotons.
Colors indicate difference in roton-magnitude. Intensity shows the gradient of the field.
This is a 2D cut from an overlapped modulation of superposed LEDO-Field. Static Rotons.
Colors indicate difference in roton-magnitude. Intensity shows the gradient of the field.
Gradient visualization
 LEDO-Field 2D cut of radial Roton oscillation paths - superposition alongside the rotational plane. Static Rotons.
Color indicates the gradient direction, intensity indicate the gradient value
LEDO-Field 2D cut of radial Roton oscillation paths - superposition alongside the rotational plane. Static Rotons.
Color indicates the gradient direction, intensity indicate the gradient value
For axial oscillation paths see further down.
Field Decomposition in the LEDO Framework
In the LEDO picture we distinguish three tightly coupled, but conceptually different, field aspects:
- A resonant potential field (ADR)
- A gyro-inertial response field (IGT)
- An energy density transition (energy-pressure) field (EDT)
Together they form the overall LEDO field, i.e. the full rotonal state of space.
If we look at the interaction of electrons as one family of Rotons then we’ll have:
- The Electric field (E) tells you how the charge (Roton with charge e) would accelerate
- The Magnetic field (B) tells you how a moving charge (Roton) will bend (precess)
- The cross-product $E \cross B$ tells you how energy escapes the system (energy/inertia flow)
1. ADR: Resonant Alignment & Amplitude Field (Resonance Field)
ADR (Axial Differential Resonance) jointly describe the static resonant landscape:
- It is a spectrally and directionally resolved field:
at each point in space we have, for each direction $\hat{n}$ and frequency $\omega$, a resonant amplitude (or its differential vector).
- It carries resonance contributions, not propagating waves.
It encodes where a given Roton, with given frequency and axis, would find a stable or unstable orientation, distance or harmonic locking.
- Physically, ADR plays the role of a potential field, analogous to an electric field / scalar potential:
- high ADR amplitude → strong tendency to align / lock
- ADR gradients → “Harmonic locking forces” on Rotons
- Energy view:
ADR encodes the configuration space of energy:
which orientations, radii and frequencies correspond to low or high rotonal energy.
It does not specify how fast the system moves there – only that these configurations are favored or disfavored.
You can think of ADR as the static resonance atlas of space.
2. IGT: Inertial Gyro-Tensor Field (Gyroscopic Field)
The Inertial Gyro-Tensor (IGT) field describes how rotonal entities actually react to changes in ADR:
- It is local, gyroscopic and inertia-bound:
each Roton carries rotational inertia and can only change its axis, frequency or phase at a finite rate.
- IGT encodes the precession delay:
for a given torque from the ADR field, IGT determines
- how much the axis can tilt per unit time,
- how quickly frequency/phase can adapt,
- which directions are “stiff” or “soft”.
- Conceptually, IGT is more like a magnetic / gyro field:
it does not define where energy minima are, but how strongly the system resists moving toward them.
- Energy view:
IGT is the kinetic side of rotonal energy:
- it stores energy in misalignment, precession and delayed response,
- it controls how potential energy (rotation) from ADR is converted into motion and internal oscillation.
ADR says: “This is where you should go.”
IGT says: “This is how hard it is to get there.”
3. Energy-Pressure Field (Qualitative)
A third aspect is an energy-pressure field (not yet fully named), which will describe:
- how energy density and its gradients push the system away from over-concentrations of energy,
- how stored rotonal energy (in ADR/DRI and IGT) is redistributed in time,
- how heat-like degrees of freedom and microscopic oscillations emerge when fine-scale misalignments are averaged out.
Qualitatively:
- ADR/DRI encodes where energy wants to sit (resonant configurations).
- IGT encodes how slowly the system can reorient to reach these configurations.
- The energy-pressure field encodes how strongly accumulated energy pushes back,
trying to flatten energy density gradients over time.
This third field is expected to be explicitly time-dependent, just as inertia (IGT) makes every adjustment inherently delayed.
4. LEDO Field: Unified Representation
The LEDO field is the combined object that, at each point in space, contains:
- the resonant alignment structure (ADR/DRI),
- the gyro-inertial response (IGT),
- and the local energy-pressure state.
In compact form:
- ADR/DRI: where resonance is favored (static, spectral, directional potential)
- IGT: how reorientation actually responds (gyroscopic, inertial delay)
- Energy-pressure: how energy gradients drive redistribution (time-dependent pressure)
Disentangling these three aspects allows us to describe:
- fields as energy landscapes (ADR/DRI),
- matter as gyroscopic carriers (IGT),
- dynamics as energy redistribution under inertia (energy-pressure).
Together, they define how rotonal entities populate space, store energy, and evolve in time within the LEDO framework.
Motivation
- In conventional physics, oscillation is often represented as a simple sinusoidal function in time or space.
- Complex systems (quantum states, coupled fields, condensed matter, or cosmological structures) rarely follow such simple oscillations.
- LEDO emphasizes interference, resonance, and overlay of multiple oscillations, producing a more lifelike, “musical” structure of energy density dynamics.
Characteristics
- Lambda or Layered: denotes the frequency aware, de-interwoven character of the oscillations (not a single pure tone).
- Energy Density: refers to the local field value of energy per unit volume, in general a fundamental scalar quantity. LEDO allows for local frequency dependent gradients.
- Oscillation: periodic or quasi-periodic modulations of single or potentially multiple overtone/harmonic frequencies.
Base field fluctuations and characteristics
The LEDO field as a whole carries oscillation potentials (kind of instantaneous waves) emerging from stable rotating structures (like photons and matter) and spreads out into different spacial directions. These waves might lead to resonances between different stable objects. Being the source for all forces between stable entities. The base waves in the LEDO field do not manifest themselves directly, unless we add another stable rotating entity with a given frequency (time aspect) at a given location. If not manifested, the LEDO field simply appears as a background noise possibly leading to small fluctuations within a given frequency range onto the manifesting entities.
Please also see the chapter on Quantization and vacuum fluctuations).
So in other words, the LEDO-Fields void ground-state mostly corresponds to the concept of “vacuum fluctuations” in standard physics.
Dispersion
Separate Note: Dispersion of LEDO-Waves read↗
Sensitivity to radial variations
Separate Note: Sensitivity to radial variations read↗
Mathematical modelling (IGT)
More precisely:
** Forces in this field are mediated via “Energy density gradients” or in Rotonal terms “Rotational Inertia Flow”. Their derivatives or modulations over time can be expressed as a local Tensor.
** The whole structure is a highly “iterative” process which might rather be investigated via simulation than via calculations of already solved formal equations.
With this tensor we are asking not only “where does energy density rise?” but “how does that rising itself bend and twist in space?”.
So the modelling might make use of an “Inertial Gradient Tensor” (IGT)

Image: Colors show amplitude
Let
$$
\rho_E(\mathbf{r},t) = \sum_i A_i(\mathbf{r}) \cos(\omega_i t + \phi_i)
$$
represent the local energy density as a superposition of modes.
Then LEDO can be understood as the effective oscillation pattern emerging from the collective superposition of such modes, i.e. the perceived rhythmic modulation rather than any single frequency.
Modeling
Energy Density as a Field
We define the local energy density as a scalar field
$$
\rho_E(\mathbf{r},t),
$$
which assigns to each point in space and time the energy per unit volume.
Gradient of Energy Density
The gradient of this scalar field is a vector field:
$$
\nabla \rho_E(\mathbf{r},t) =
\left(
\frac{\partial \rho_E}{\partial x},,
\frac{\partial \rho_E}{\partial y},,
\frac{\partial \rho_E}{\partial z}
\right).
$$
- Units: energy per volume per length.
- Interpretation: direction and magnitude of steepest increase in local energy density.

Image: Colors show gradient
Gradient Tensor (Hessian)
The derivatives of this gradient form a rank-2 tensor, i.e. the Hessian:
$$
H_{ij} = \frac{\partial^2 \rho_E}{\partial x_i \partial x_j}.
$$
- Encodes the curvature of the energy density field.
- Describes how the gradient itself changes in different spatial directions.
- Eigenvalues/eigenvectors of (H_{ij}) indicate principal directions of curvature (maxima, minima, saddle points).
Physical Significance
- Fluid dynamics analogy: velocity gradient and stress tensors describe shear/expansion; the Hessian plays a similar role for energy density fields.
- General relativity analogy: covariant derivatives of the stress-energy tensor (T_{\mu\nu}) encode conservation and curvature effects.
- Field theory: the Hessian of an energy functional governs stability, mass matrices, and dispersion relations.
Summary
- Gradient: vector field of energy density changes.
- Gradient tensor (Hessian): rank-2 tensor describing curvature of energy density.
- Physically meaningful as a tool to analyze in-homogeneity and local stability in energy distributions.

Image: This image shows a planar intersection of the LEDO waves within the rotation plane. We see different Rotons emitting radial waves into the LEDO-Field.
Colors: Colors show overall gradient vector direction. Hue is the local gradient value.
Relation to Known Concepts
- Similar to Lissajous figures: LEDO describes not only the existence of multiple frequencies but their interplay.
- Extends beyond linear superposition by allowing resonant amplification or beating patterns (constructive/destructive).
- Bridges physics and metaphor: conveys that energy density oscillations may carry musical, rhythmic qualities.
Potential Applications
- Quantum models: describing interference of multiple oscillatory field contributions.
- Condensed matter: collective excitation (phonons, magnons) with nontrivial superposition.
- Cosmology: oscillations in primordial fields, dark energy modulation, or “beats” in large-scale structure formation.
- Roton-inspired models: LEDO captures the resonance-driven, non-point-like nature of energy density oscillations.
Summary Statement
LEDO (Lambda Energy Density Oscillation) provides a metaphorically enriched yet mathematically precise concept for describing interwoven, resonant oscillations of local energy density, transcending simple harmonic motion and highlighting the emergent rhythmic character of complex systems.

Image: This image shows a perpendicular intersection of how Rotons of different sizes emit waves in axial direction (perpendicular to the rotation plane) into the LEDO-Field.
Colors: Colors show gradient vector direction. Hue is the gradient value.
The Rotonic Model: A Taxonomy of Rotational Entities
In a reality where spin is sacred and symmetry whispers across spacetime, we distinguish several classes of rotational entities. These objects, conceptual or real, emerge from the primordial rotational essence: the Roton. From there, configurations become more complex, layered, and deceptive in their simplicity.
| Name |
Description |
Property |
Metaphor |
| Roton |
The elemental unit of rotation; indivisible and pure |
Fundamental, isolated |
A single musical note suspended in vacuum |
| Di-Roton |
A resonant coupling of two Rotons; minimal rotational pair |
Dual interaction, coherent binary state |
An entanglement; an attractive force |
| Rotron |
A composite of overlapping co-planar and co-centric Rotons. They might feel like a disguised simple Roton |
Condensed multi-structure in disguise |
An orchestra chord pretending to be a single tone. Additional attraction caused by co-axial rotation. |
| Gyrotron |
A co-centric system of multiple Rotons, specifically not co-planar; with rotation axis pointing in 3 different spacial directions |
Organized, radiant structure |
The basis for a stable entity in space. |
| Di-Gyrotron |
Two entangled Gyrotrons; long-distance synchronization and coupling |
Macroscopic quantum resonance |
This seems less coupled than a Di-Rotron (not introduced yet ;-) , which might have more attractive forces. |
“Where particles are poetry and spin is structure,
the Roton sings first, but the Gyrotron brings the echo across spacetime.”








Use the share button below if you liked it.
It makes me smile, when I see it.