Energy optimization in atoms
Why do protons and electrons build atoms? Imagine 2 stationary (central) protons and two electrons.
What happens:
- As they are rotating, both electrons and protons attract each other (in nearly the same way).
- The LEDO-Field “wind” blows them apart so the electrons adjust oposite each other stationary around the proton. Attraction equals repulsion.
- Now the electrons start to move influenced by the LEDO-Field fluctiations. As they start rotating the build a roton. This way they get attracted closer to the protons.
- Looking at a Helium-Atom with 4 rotating electrons in a plane you can see and understand from the Roton model, that there is some attraction between these two phase-synchoneous Rotons of different sizes (Factor <4).
- Now what about the H-Atom? It seems that even a single electron manages to get closer to the proton by rotating around it.
- Now it gets really interesting, because this implies, that even a “self-rotation” can induce a rotonal attraction to ones own rotation center.
- A kind of self-resonance in the LEDO-Field.
Furthter consideration:
- So why does the electron not fly away when rotating? Because it is attracted by the nucleus (rotonally). So as long as its speed does not increase a certain level, we are all fine.
- The electrons around the protons try to find the optimal rotational states so they can come as close as possible to the center. Hereby increasing energy density.
- Does an electron “want” something by itself? No. It simply fails to leave the influence of a stronger attraction, as soon as it gets occasionally caught by it. The electron basically falls into the pod of higher attraction and denser energie while still beeing held back by the wave pressure in the LEDO-Field wind.
- The universe is a constant way of optimizing itself. With more or less success. Every fluctuation here and there drags another ompimal state out of the optimom bumbing around
- Maximizing energy density is minimizing local entropy and maximizing global Entropy. Both are limitted to the scale at which we look at the system so rather a “Ignorance measure of indistinguishability”
- An electron has an entropy of 0 because it has only one state - but wait it has a spin? So minimizing entropy is minimizing the ignorance of indistinguishability.
- Entropy is the quantitative measure of your blindness to hidden distinctions in the system.
Distribution and Orientation of Electron-Rotons within Atoms
Introduction
This chapter focuses on how the Rotonal model might explain the basic Atomic structures. We will look at different constellations and how to build an energetically optimal stable state.
Let me give one important prelude:
- The Quantum-Mechanics atom model assumes, that the orbitals (1s, 2s, 2p, 3s, 3p, 3d, 4s …) are the wavefunctions of an electron or the probability distribution of “where to find” an electron when you try to measure it.
- Measuring changes/influences an atom though. So the resulting measurement will only show the reaction of the system to external influences.
To be really precise we’d need to say:
- Atom orbitals are ONLY the resonances of the atom, which we are bumping with different photons of specific sizes/energies.
- We do not actually “know” how the structure or probability distrubution of the electrons in an atom IS when it is left alone.
And having a look at the instable excitations into other orbitals, it seems there are other forms of “rotations” an electron can choose around a nucleus.
Roton types and orientations
As surely stated in other parts Rotons can come with several (maybe temporal) stable constellations.
| Roton Coupling type | Spin orientation | Standard Term | Resonance/Force | Roton orientations | Spin Locking |
|---|---|---|---|---|---|
| Co-Axial (Entangl.) | Oposite Co-Axial | Antiparallel spins | Big Attractive | o→ ←o ↦ ↤ | strong |
| Co-Axial (Repulsi.) | Concurrent Co-Axial | Parallel spins | Big (Repulsive) | o→ ←o ↦ ↤ | strong |
| Parallel | Up/Up or Down/Down | Parallel | Medium | ↑↑, ↓↓ | medium |
| Anti-Parallel | Up/Down or Down/Up | Antiparallel | Medium | ↑↓, ↓↑ | medium |
| Unaligned | Arbitrary, unaligned | Misaligned, skew ? | Small (Gravitation) | ↑↗︎→↘︎ | none |
This definitions/values come from interpretation of the observations with field directions and forces between two magnets of different orientations.
Rotonal combinations in atoms
H-Atom:
- The Electron and the Proton build an (uneven) rotonal coaxial connection. They build an entanglement, so their rotation axis are kept synchronous.
- Depending on external influences
He-Atom:
- The two electrons (an electron-pair) take oposite sides to each other with oposite coaxial orientations.
- In combination with the electron<->proton coupling this further increases attraction between electrons and leads to more optimal energetic positions.
- External influences can lift electrons to higher energy levels (distance to nucleus). If a single electron is lifted (excited), they loose the entanglement.
- Electrons on different energy levels (shells) loose their entanglement and coaxial orientation, as they will take different rotation speeds (1/n^2 distances)
- They might tend to align themselves linearly (parallel, antiparallel) to still optimize for energy-density.
- Once both electrons reach the higher energy level, they might remain in this intermediate parallel/antiparallel state for a while.
- If this temporal stability is somehow disturbed (e.g. temperature?) the electrons will first find an unaligned orientation until the LEDO-Field base fluctuations lead the electrons into locked coaxial orientations.
- Once reaching coaxial orientation again, they will drop back to the base level with the highest energy density.
| He Groundstate $1s^2$ | He Excited parallel / triplet | He excited coaxial / singlet |
|---|---|---|
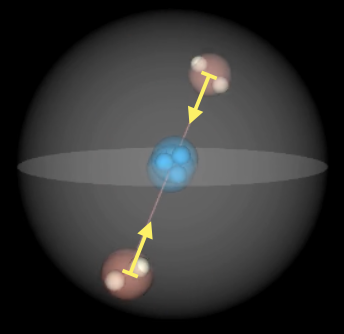 |
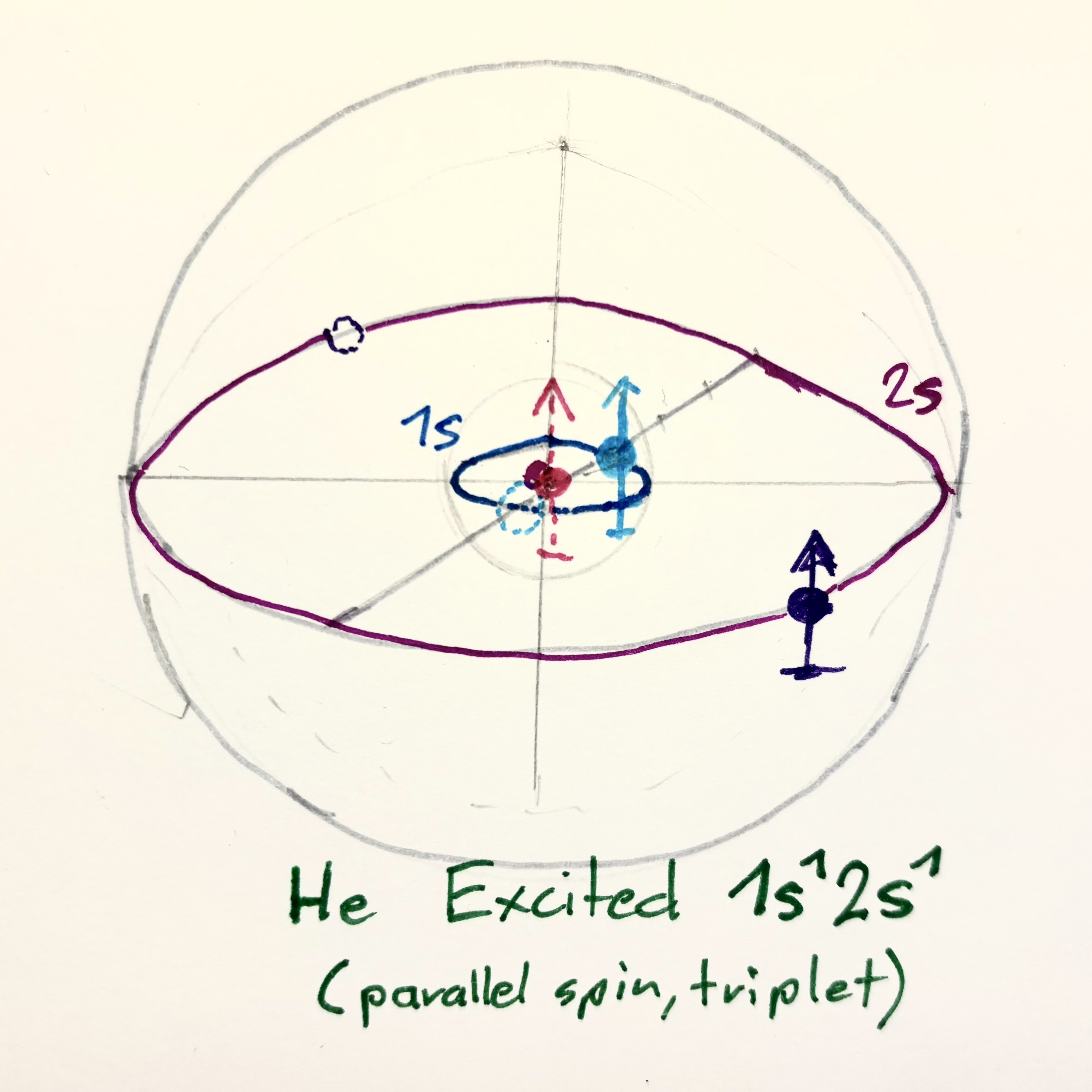 |
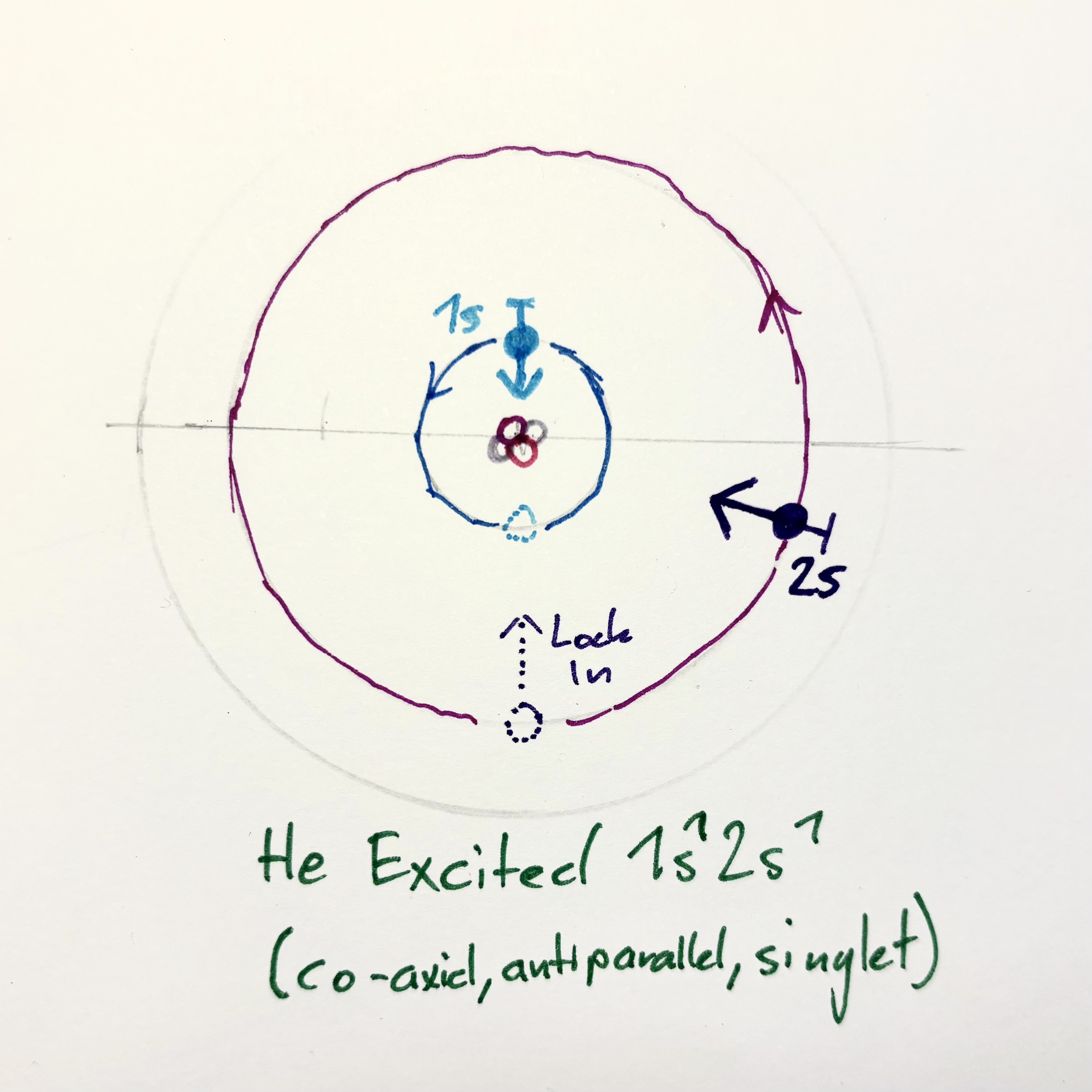 |
This is how the Roton model would explain behavior and stability of exitation of electrons to upper shells.
Verification with the standard atom model
Helium: Electron Spin Orientations (1s and 2s)
Ground state: 1s²
- Both electrons in the 1s orbital
- Must have opposite spins (Pauli exclusion principle)
- Spin singlet (S = 0):
1s: ↑↓
Excited states: 1s¹ 2s¹
- One electron in 1s, one in 2s
Case 1: Antiparallel spins (singlet)
1s: ↑, 2s: ↓
- Allowed
- Lower in energy
Case 2: Parallel spins (triplet)
1s: ↑, 2s: ↑
- Allowed
- Higher in energy, often metastable
- Transition to ground state is spin-forbidden
Forbidden configuration
- Two electrons in the same orbital with identical spin
- Example: 1s: ↑↑
- Not allowed (violates Pauli exclusion principle)
Summary Table
| Configuration | Spins | State | Allowed? | Comment |
|---|---|---|---|---|
| 1s² | ↑↓ | Singlet | ✅ Yes | Ground state, stable |
| 1s² | ↑↑ or ↓↓ | — | ❌ No | Forbidden by Pauli principle |
| 1s¹ 2s¹ | ↑↓ or ↓↑ | Singlet | ✅ Yes | Excited state, lower energy, short-lived |
| 1s¹ 2s¹ | ↑↑ or ↓↓ | Triplet | ✅ Yes | Excited state, higher energy, metastable |
| 1s¹ 2p¹ | ↑↓ or ↓↑ | Singlet | ✅ Yes | Excited, short-lived |
| 1s¹ 2p¹ | ↑↑ or ↓↓ | Triplet | ✅ Yes | Excited, metastable, important in spectroscopy |
Assessment of the Roton Model
The Roton model provides a compelling framework to explain why specific positional constellations of electrons are energetically more favorable than others, and why certain arrangements naturally stabilize. Rather than declaring that a configuration is “forbidden,” the model demonstrates that it is simply less favorable compared to the energetically preferred alternatives. In this way, stability emerges as a natural consequence of energetic optimization, not as an imposed rule. The Roton model thus offers not only a consistent explanation, but also an intuitive picture of why electrons arrange themselves in these particular ways.
Take this phrase from Standart Physics: “Two electrons in the same orbital with identical spin are forbidden” Why is this?
Use the share button below if you liked it.
It makes me smile, when I see it.